Curl of a vector field (Curl given)
Aim of task
- Student knows how to calculate partial derivatives, vector products and curls of 3D vector fields (Handling mathematical symbols and formalism)
- Student understands, how a vector field and its curl are connected graphically (Representing mathematical entities)
- Using a visualization of vector field and its curl the student can graphically check whether his calculations are correct (Making use of aids and tools)
 |
|---|
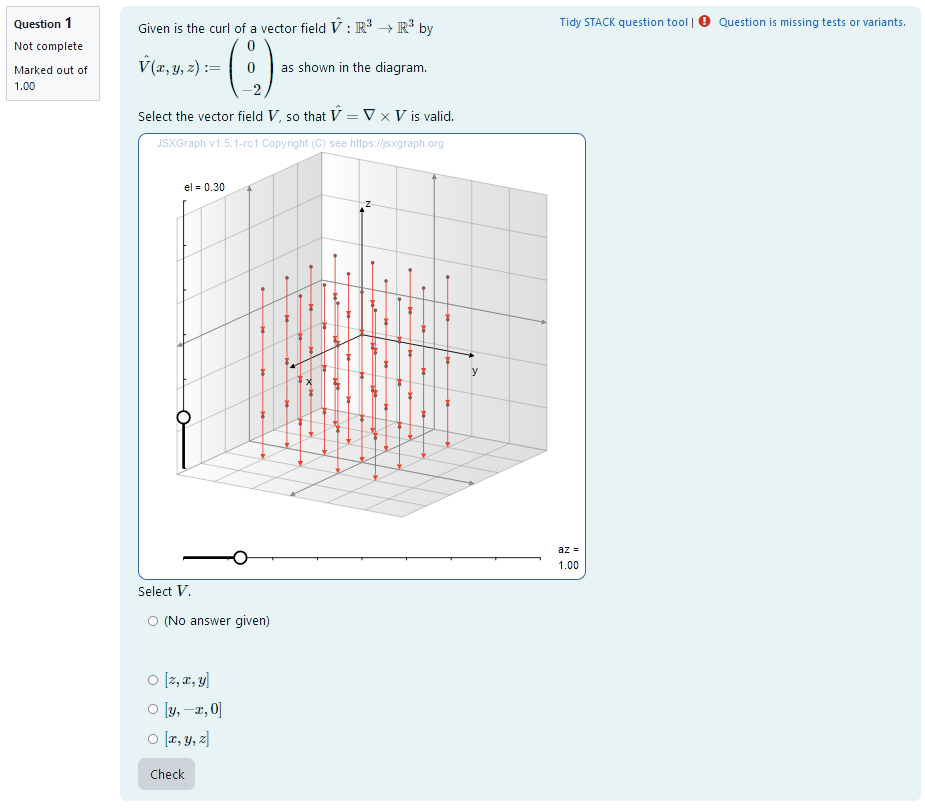
| First impression of the question |
Question description
A 3D vector field is plotted. It is the curl of another vector field. 3 different options for this field are presented in the form of radio buttons and the student needs to pick what they believe to be correct.
Student perspective
The student sees a plot of the 3D vector field. They can rotate their point of view using the sliders and get a better idea of the vector field.
 |
|---|
| When the student solves the problem |
Teacher perspective
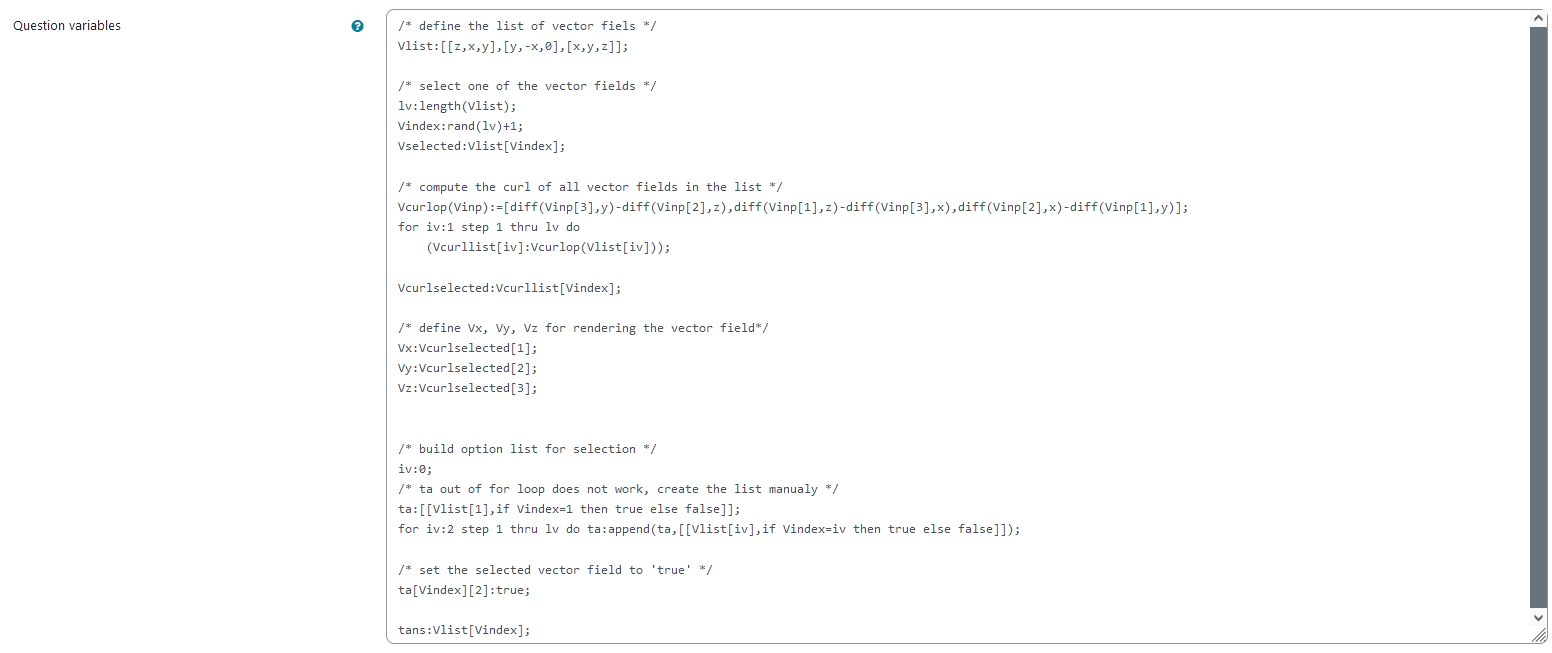
The teacher can remove entries from or add entries to the list Vlist that contains the vector fields. Possible vector fields need to contain only the variables x, y and z. The coordinates are saved in the shape [x-component, y-component, z-component]. Each of the components can be dependent on all variables.
The rest of the Question variables should not be altered.
 |
|---|
| The above image shows which values the teacher may wish to change |
Question code
Question Variables
- Vlist is a list of 3D vector fields dependent on x,y,z and constants given in format [f_x,f_y,f_z] to randomly select from
- Select one of the vector fields by randomizing the index Vindex of the list and evaluating Vlist via Vselected: Vlist[Vindex]
- Define Variables Vx, Vy, Vz as the vector field components in order to plot it in Question text
- Save the curls of all of the vector fields with attribute false to a list in order to access it in Question text
- Set attribute of curl of selected vector field to true in order to be able to check answer
Question variable code
/* define the list of vector fields */
Vlist:[[z,x,y],[y,-x,0],[x,y,z]];
/* select one of the vector fields */
lv:length(Vlist);
Vindex:rand(lv)+1;
Vselected:Vlist[Vindex];
/* compute the curl of all vector fields in the list */
Vcurlop(Vinp):=[diff(Vinp[3],y)-diff(Vinp[2],z),diff(Vinp[1],z)-diff(Vinp[3],x),diff(Vinp[2],x)-diff(Vinp[1],y)];
for iv:1 step 1 thru lv do
(Vcurllist[iv]:Vcurlop(Vlist[iv]));
Vcurlselected:Vcurllist[Vindex];
/* define Vx, Vy, Vz for rendering the vector field*/
Vx:Vcurlselected[1];
Vy:Vcurlselected[2];
Vz:Vcurlselected[3];
/* build option list for selection */
iv:0;
/* ta out of for loop does not work, create the list manualy */
ta:[[Vlist[1],if Vindex=1 then true else false]];
for iv:2 step 1 thru lv do ta:append(ta,[[Vlist[iv],if Vindex=iv then true else false]]);
/* set the selected vector field to 'true' */
ta[Vindex][2]:true;
tans:Vlist[Vindex];
Question Text
-
Given is the curl of a vector field $\hat V:\mathbb{R}^3\to\mathbb{R}^3$ by $\hat V(x,y,z):=\begin{pmatrix}{@Vx@}\{@Vy@}\{@Vz@}\end{pmatrix}$ as shown in the diagram. Select the vector fields $\hat V$, so that $\hat V = \nabla \times V$ is valid.
- JSXGraph applet using the functions and variables defined in Question variables plotting the 3D vector field and its curl in a projected plane, the angle of projection can be changed such that the vector fields can be viewed from multiple directions
[[input:ans1]]at the end of JSXGraph code to allow input of an answer of the student[[validation:ans1]]checking of answer
Question text code
<p>Given is the curl of a vector field \(\hat V:\mathbb{R}^3\to\mathbb{R}^3\) by \(\hat V(x,y,z) := \begin{pmatrix}{@Vx@} \\ {@Vy@} \\ {@Vz@}\end{pmatrix} \) as shown in the diagram.</p>
<p>Select the vector field \(V\), so that \( \hat V = \nabla \times V\) is valid.</p>
[[jsxgraph width="500px" height="500px" input-ref-ans1='ans1Ref']]
var board = JXG.JSXGraph.initBoard(divid,{boundingbox : [0, 10, 10,0], axis:false, shownavigation : false});
var box = [-3,3]
var view = board.create('view3d',
[[2,2.5], [6, 6],
[box, box, box]],
{});
// Transform components of the vector function
var TF1 = board.jc.snippet('{#Vx#}', true, 'x,y,z');
var TF2 = board.jc.snippet('{#Vy#}', true, 'x,y,z');
var TF3 = board.jc.snippet('{#Vz#}', true, 'x,y,z');
var vector=[];
var scaleVec = 0.5;
/* Funktionen zum Plotten der Vektorfelder */
function clearVectorField(){
board.removeObject(vector);
vector=[];
}
function vectorField(){
clearVectorField();
board.suspendUpdate();
var i,j,k,vx,vy;
var pout=[];
for(k=-2; k<2; k+=1){
for(i=-2; i<2; i+=1){
for(j=-2;j<2; j+=1){
//var norm = Math.max((i*i+ j*j ),0.001);
var norm =1;
vector.push(view.create('line3d',[[i, j,k ],
[TF1(i,j,k),TF2(i,j,k),TF3(i,j,k)],[0,scaleVec]],
{point: { withLabel: false},
point1: {visible: true, size: 1, color: '#EE442F',strokeColor: '#EE442F', withLabel: false},
point2: {visible: false, withLabel: false},
lastArrow:true, fixed: true, strokeColor:'#EE442F', highlight:false})
);
}
}
}
board.unsuspendUpdate();
}
/* end helper functions */
vectorField();
board.update();
/* axis labels*/
var xlabel=view.create('point3d',[0.9*box[1],0,(0.6*box[0]+0.4*box[1])], {size:0,name:"x"});
var ylabel=view.create('point3d',[0,0.9*box[1],(0.6*box[0]+0.4*box[1])], {size:0,name:"y"});
var zlabel=view.create('point3d',[
0.7*(0.6*box[0]+0.4*box[1]),
0.7*(0.6*box[0]+0.4*box[1]),
0.9*box[1]],
{size:0,name:"z"});
[[/jsxgraph]]
Select \( V\).
<p>[[input:ans1]] [[validation:ans1]]</p>
Answers
Answer ans 1
|property | setting|
|:—|:—|
|Input type |Radio|
|Model answer | ta defined in Question variables |
| Forbidden words | none |
| Forbid float | No |
| Student must verify | Yes |
| Show the validation | Yes, compact|
—
General feedback
<hr>
<p> The notation \(\nabla \times V\) is describing the application of the curl operator on a vector field \(V\). It is based on the notation of the gradient of a potential \(f\) given as \(\nabla f = \begin{pmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y}\\ \frac{\partial f}{\partial z} \end{pmatrix}\). </p>
<p> The curl is then defined by the vector product of the nabla operator \(\nabla = \begin{pmatrix} \frac{\partial }{\partial x} \\ \frac{\partial}{\partial y}\\ \frac{\partial}{\partial z} \end{pmatrix}\) and the vector field \(V = \begin{pmatrix} V_x \\ V_y \\V_z \end{pmatrix}\).</p>
<p> We find \(\nabla \times V = \begin{pmatrix}\frac{\partial V_z}{\partial y}- \frac{\partial V_y}{\partial z}\\ \frac{\partial V_x}{\partial z}- \frac{\partial V_z}{\partial x} \\ \frac{\partial V_y }{\partial x}- \frac{\partial V_x}{\partial y} \end{pmatrix} \). </p>
Potential response tree
prt1
 |
|---|
| Visualization of prt1 |
Feedback variables:
None needed, since ans1 is selected by ticking a button.
 |
|---|
| Values of node 1 |
Node 1
| property | setting |
|---|---|
| Answer Test | AlgEquiv |
| SAns | ans1 |
| TAns | tans |
| Node 1 true feedback | <p>Nice! You found the correct vector field. \(\hat V\) is the curl of this field.</p> |
| Node 1 false feedback | <p>You did not select the correct vector field. The vector field given is the curl of the wanted vector field.</p> |
 |
|---|
| Values of node 1 |